Расчет параметров треугольника

Равенство треугольников

Теорема 19. Два треугольника равны, если три стороны одного соответственно равны трем сторонам другого.

Дано. В двух треугольниках ABC и DEF (черт. 43) стороны равны

AB = DE, BC = EF, AC = DF

Требуется доказать, что ∆ABC = ∆DEF.

Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC точкой D на точку A. По равенству сторон AC и DF точка F упадет на точку C.

Чтобы доказать, что точка E упадет на точку B докажем, что она не может упасть ни внутри, ни вне, ни на одну из сторон треугольника.

a) Положим, что точка E упадет внутри треугольника в точку E’, тогда треугольник DEF примет положение треугольника AE’C, DE займет положение линии AE’ и EF положение линии E’C, следовательно,

AE’ = DE, E’C = EF.

Линия ABC, будучи внешней ломаной, больше линии AE’C внутренней ломаной, следовательно,

AB + BC > AE’ + E’C

Заменяя AE’ и E’C равными им сторонами DE и EF, имеем:

AB + BC > DE + EF,

но AB = DE, следовательно, BC > EF, что противоречит данным условиям. Итак, точка E не может упасть внутри треугольника.

b) Положим, точка E упала вне треугольника в точку E». В этом случае ∆AE»C = ∆DEF и тогда

AE» = DE, CE» = EF

Обозначим букой O точку пересечения линий AE» и BC. Из чертежа видно, что

AO + BO > AB
CO + OE» > E»C

Сложив эти неравенства, имеем:

AO + BO + CO + OE» > AB + E»C

Так как BO + CO = BC, AO + OE» = AE», то

BC + AE» > AB + CE»

Здесь AE» = DE, CE» = EF, следовательно,

BC + DE > AB + EF

но AB = DE.

Вычтя по равной величине из обоих частей последнего неравенства, получаем:

BC > EF

что противоречит данным условиям. Итак, точка E не может упасть вне треугольника.

c) Точка E не может упасть на одну из сторон треугольника в точку E»’, ибо стороны DC и AB равны. Точно также если бы E упала в точку O, то выходило бы, что BC > OC, но OC = EF, следовательно, BC > EF, что противоречит условию.

Итак, точка E должна непременно упасть в точку B, следовательно, при наложении сторона DE совпадет со стороной AB, а сторона EF со стороной BC и треугольник DEF с треугольником ABC.

Из равенства треугольников следует, что все остальные части их равны, т. е.

∠A = ∠D, ∠B = ∠E, ∠C = ∠F.

Теорема 20. Два треугольника равны, когда они имеют по равному углу, содержащемуся между равными сторонами.

Дано. В двух треугольниках ABC и DEF (черт. 44)

AB = DE, AD = DF, ∠BAC = ∠EDF

Требуется доказать, что ∆ABC = ∆DEF.

Примечание. Иногда указывают равные части на чертеже, отмечая их одинаковыми значками.

Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC, точкой D на точку A; тогда по равенству линий DF и AC точка F упадет в точку C и по равенству углов A и D линия DE пойдет по линии AB; по равенству линий DE и AB точка E упадет на точку B. Если E и F две точки линии EF совпали с B и C двумя точками линии BC, то и вся линия EF совпадет с линией BC, и треугольник DEF совпадет с треугольником ABC. Отсюда следует, что и все остальные части треугольников равны, т. е.

BC = EF, ∠B = ∠E, ∠C = ∠F.

Теорема 21. Два треугольника равны, если сторона и два лежащие на ней угла одного равны стороне и двум лежащим на ней углам другого треугольника.

Дано. В треугольниках ABC и DEF (черт. 44)

∠A = ∠D, ∠C = ∠F, AC = DF

Требуется доказать, что ∆ABC = ∆DEF.

Доказательство. Наложим треугольник DEF на треугольник ABC, стороной DF на AC, точкой D на A, тогда по равенству сторон AC и DF точка F упадет на точку C. По равенству углов A и D линия DE пойдет по линии AB и по равенству углов C и F линия FE пойдет по линии CB. Так как линия FE и DE совпадут с линиями CB и AB, то и точка E непременно совпадет с точкой B, ибо две прямые линии пересекаются в одной точке, следовательно два треугольника равны (ЧТД).

Из того, что равные треугольники совмещаются при наложении всеми своими частями вытекает следствие. В равных треугольниках против равных сторон лежат равные углы и наоборот.

Соответственные части треугольников. В двух равных треугольниках равные углы и равные стороны называются соответственными углами и сторонами.

Свойства внешних углов

Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.

Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:

а+в+с=180

а+d=180

Вычтем из первого выражения второе и получим:

а+в+с-(а+d)=180-180

в+с-d=0

d=в+с – вот и все доказательство.

Рис. 2. Рисунок к доказательству.

Есть еще несколько дополнительных свойств внешних углов:

• Если решение задачи требует одновременного существования двух внешних углов при одной вершине на чертеже, то можно заметить, что эти внешние углы будут равны, как вертикальные.
• Сумма трех внешних углов, по одному при каждой из вершин, равна 360 градусам.
• Так как внешний и внутренний углы треугольника смежные, то их сумма равна 180 градусам.

Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.

Рис. 3. Внешний угол тупоугольного треугольника.

Что мы узнали?

Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.

1. /5

   Вопрос 1 из 5

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

Существует три вида треугольников по углам:

• остроугольные;
• прямоугольные;
• тупоугольные.

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90.

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.

Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

Рис. 2. Виды треугольников по углам.

Пифагоровым треугольником называется прямоугольный треугольник, стороны которого равны 3, 4, 5.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3 и 4, то третья обязательно будет 5, и треугольник непременно будет прямоугольным. Это упростит расчеты.

Виды треугольников по сторонам:

• равносторонние;
• равнобедренные;
• разносторонние.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60, то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины сторон и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

Рис. 3. Виды треугольников по сторонам.

Сумма всех углов треугольника, независимо от его вида, равна 180 градусам.

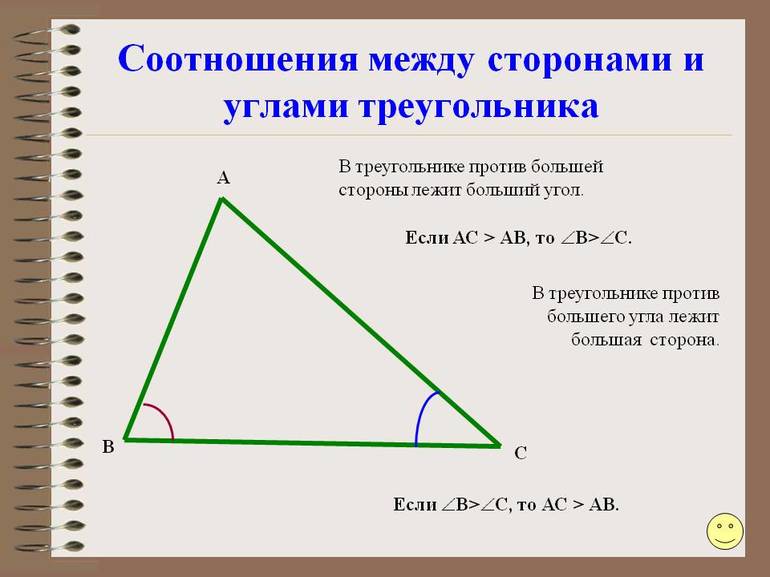
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основанию и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.

О многоугольнике с тремя сторонами

Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.

Таким образом, два ключевых элемента образуют рассматриваемую фигуру:

• вершина;
• сторона.

И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.

На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.

Существование фигуры

Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.

Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.

Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:

1. Остроугольные. В них все три угловые меры меньше 90 °. При этом возможны случаи взаимного их равенства, то есть каждый будет составлять 60 °. Такие треугольники называются равносторонними или правильными. Равны могут быть между собой также два угла, это будет уже равнобедренный треугольник, у которого боковые стороны имеют одинаковую длину.
2. Тупоугольные. Поскольку сумма составляет 180 °, то по определению в рассматриваемом многоугольнике не может быть больше одного тупого угла. Тупоугольные фигуры могут иметь либо произвольный тип, когда все их отрезки различаются, либо являться равнобедренными.
3. Прямоугольные. Это специальный тип треугольников, о котором известно многое, и который разграничивает два предыдущих типа. В них один угол равен 90 °, а два других являются острыми.

Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.

Важные линии

Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:

1. Медиана — делящий на две равные по площади части исходный треугольник. Отрезок проводится из вершины к середине противоположной стороны.
2. Биссектриса. Ею называют отрезок, который на две половины делит угол при произвольной вершине.
3. Высота. Этот элемент проводится также из вершины, но по отношению к противоположной стороне он является перпендикуляром. Таким образом, высота делит исходную фигуру на два прямоугольных геометрических объекта, которые в общем случае между собой не равны.
4. Медиатриса — это серединный перпендикуляр, то есть он сочетает свойства медианы и высоты, однако, через вершину треугольника он может не проходить. Медиатрисами пользуются при построении описанной окружности.
5. Средняя линия — это отрезок, который посередине пересекает две стороны треугольника. Его длина всегда будет в два раза меньше стороны фигуры, которой он параллелен. Средняя линия приводит к созданию подобной исходной фигуры, которая в два раза меньше.

Теорема неравенства треугольника: задачи

Задача #1. В треугольнике одна сторона в три раза меньше суммы двух других. Докажите, что против этой стороны лежит наименьший угол треугольника.

Дано:$a, b, c$$3a=b+c$

Найти:$a<b$, $a<c$

Решение. По теореме о соотношениях между сторонами и углами известно, что против меньшей стороны лежит меньший угол. Следовательно, нам достаточно доказать, что $a$ — наименьшая из сторон в треугольнике. Раз она наименьшая, против нее будет лежать наименьший угол. Согласно теореме неравенства треугольника имеем следующие соотношения между сторонами $a$, $b$ и $c$:

$$a<b+c\\b<a+c\\c<a+b$$

Выразим сторону $b$ через стороны $a$ и $c$ в тождестве $3a=b+c.$ Получается: $b=3a-c$. Подставим полученное значение для стороны $b$ в неравенство $b<a+c$:

$$3a-c<a+c\\2a<2c\\a<c$$

Искомая сторона меньше стороны $c$. Для того, чтобы доказать, что она также меньше стороны $b$, выразим сторону $c$ через стороны $a$ и $b$ в тождестве и подставим полученное значение в неравенство $c<a+b$:

$$3a-b<a+b\\2a<2b\\a<b$$

Сторона $a$ меньше и стороны $b$, и стороны $c$. Что и требовалось доказать.

Самостоятельная практика

Следующая задача — для самостоятельного решения. Совсем немного логики и все получится. Если не справитесь, готовое решение скрыто под условием.

Задача #2. В. треугольнике длины двух сторон равны $3,14$ и $0,67$. Найдите длину третьей стороны, если известно, что она является натуральным числом.

{"questions":}

Показать решение

Скрыть решение

Дано:$b=3,14$$c=0,67$$a\in\mathbb{N}$

Найти: $a$ — ?

Решение. Чтобы найти длину третьей стороны, воспользуемся неравенством треугольника $a<b+c$, где $a$ — искомая сторона, $b$ и $c$ — заданные по условию стороны. Получается, что длина третьей стороны:

$$a<3,14+0,67\\a<3,81$$

$a$ — натуральное число, меньше $3,81$. Можно воспользоваться методом перебора (у нас не так много вариантов: $1\leq{a}\leq{3}$), но что, если бы вариантов было не три, а несколько сотен? Поэтому целесообразнее воспользоваться обратным неравенством треугольника: $a>b-c$. Тогда выходит:

$$2,47<a<3,81$$

Раз $a\in\mathbb{N}$, делаем вывод, что $a=3$.

Ответ: 3.

Внешний угол

Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равна 180 градусам. Смежными углами зовутся углы, одна из сторон каждого лежит на одной прямой, а вторая является общей.

Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых, и смежных углов будет два.

Рис. 1. Внешние углы треугольника.

Итого в треугольнике получается 6 внешних углов.

Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.

Неравенство треугольника для разности

Итого, мы установили, что сумма длин двух сторон треугольника всегда больше длины третьей стороны. Но что, если посмотреть на неравенство треугольника не как на сумму, а как на разность? Давайте попробуем выразить каждую сторону в неравенствах ($\textcolor{purple}{b}+\textcolor{orange}{c}>a,~\textcolor{green}{a}+\textcolor{orange}{c}>b,~\textcolor{green}{a}+\textcolor{purple}{b}>c$) через разность и посмотрим, что у нас получится.

Внимание на цветовую разметку:

$$\textcolor{purple}{b}>a-c\\\textcolor{orange}{c}>a-b\\\textcolor{green}{a}>b-c$$

$$\textcolor{purple}{b}>c-a\\\textcolor{orange}{c}>b-a\\\textcolor{green}{a}>c-b$$

Рассмотрим, к примеру, последнюю пару неравенств $a>b-c$ и $a>c-b$. При условии, что буквенные обозначения задают длины сторон треугольника, есть ли принципиальная разница между выражением $b-c$ и выражением $c-b$? Конечно нет. Длина стороны треугольника не бывает отрицательной. Поэтому имеем следующее:$$|b-c|=|c-b|$$Следовательно, неравенство треугольника для разности можно сформулировать так:  

{"questions":[{"content":"В треугольнике сторона $a$ равняется $6$, сторона $b$ равняется $8$. Чему равняется сторона $c$, если известно, что $c>12$ и $c\\in\\mathbb{Z}$? `input-1`","widgets":{"input-1":{"type":"input","answer":"13"}},"step":1,"hints":["Воспользуемся неравенством треугольника и обратным неравенством треугольника:$$8-6 < c < 8+6$$","По условию $c>12$. Раз $c$ — целое число, то $c=13$.","<b><i>Ответ</i></b>: 13."]}]}

Виды треугольников

Треугольники можно разделять на различные виды по углам и по сторонам треугольника. Рассмотрим для начала, какие бывают виды треугольников в различии от их углов.

Треугольник будем называть остроугольным, если все углы в нем менее 900.

Треугольник будем называть тупоугольным, если один из углов в нем более 900.

Треугольник будем называть прямоугольным, если один из углов в нем равен 900.

Все эти виды изображены на рисунке 2.

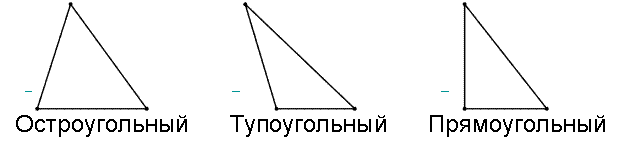Рисунок 2. Виды треугольников. Автор24 — интернет-биржа студенческих работ

По сторонам треугольники разделяются на разносторонние, равнобедренные и равносторонние.

Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.

Треугольник будем называть равносторонним, если три его стороны будут равны между собой.

Все эти виды треугольников изображены на рисунке 3.

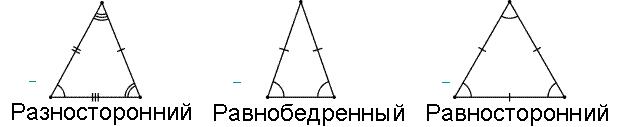Рисунок 3. Виды треугольников. Автор24 — интернет-биржа студенческих работ

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон. 

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

S = p∗r

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5

Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6

У правильного треугольника все внешние биссектрисы параллельны сторонам;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Треугольник устойчив на любой своей стороне – то есть чтобы вывести его из состояния равновесия надо приложить силу.

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

, или .

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10<15, то есть треугольник не получится.

А вот такие длины сторон 5 см, 7 см и 6 см вполне могут образовать треугольник: складываем 5+6=11 и 11>7  – треугольник с такими длинами сторон существует.

Правило встречается в следующих упражнениях:

5 класс

Задание 626,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 952,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1685,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1810,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 7,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Задание 902,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Задание 2.139,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Номер 338,
Мерзляк, Полонский, Якир, Учебник

Номер 1194,
Мерзляк, Полонский, Якир, Учебник

Номер 9,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 684,
Мерзляк, Полонский, Якир, Учебник

Номер 713,
Мерзляк, Полонский, Якир, Учебник

Номер 720,
Мерзляк, Полонский, Якир, Учебник

Номер 1184,
Мерзляк, Полонский, Якир, Учебник

Номер 1266,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Задание 259,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1409,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1571,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 753,
Мерзляк, Полонский, Якир, Учебник

Номер 980,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 433,
Мерзляк, Полонский, Якир, Учебник

Номер 453,
Мерзляк, Полонский, Якир, Учебник

Номер 456,
Мерзляк, Полонский, Якир, Учебник

Номер 459,
Мерзляк, Полонский, Якир, Учебник

Номер 676,
Мерзляк, Полонский, Якир, Учебник

Номер 677,
Мерзляк, Полонский, Якир, Учебник

Свойства треугольников

Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.

Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.

Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.

Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.

Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.

Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.

Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.

Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.

Следующие две теоремы рассматривают свойства для равнобедренных треугольников.

Углы при основании равнобедренного треугольника будут равными.

Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.

Замечание 1

Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.

Внешние углы треугольника

Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:

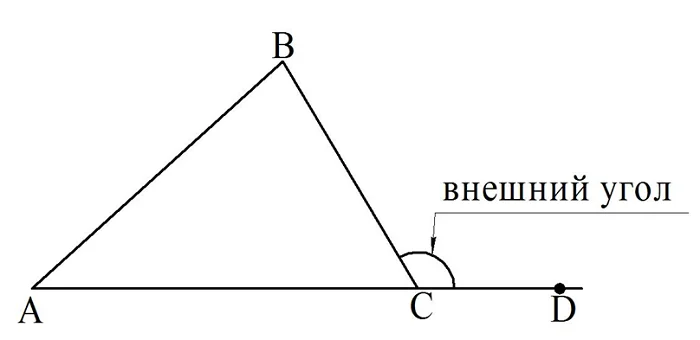
На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются . Это позволяет нам дать следующее определение:

В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.

Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.

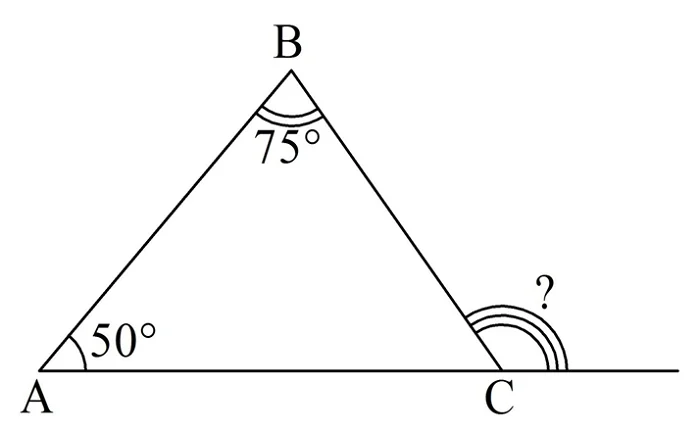
Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:

Рассмотрим ещё несколько более тяжелых задач.

Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.

Решение. Устно такую задачу не решить, поэтому построим рисунок:

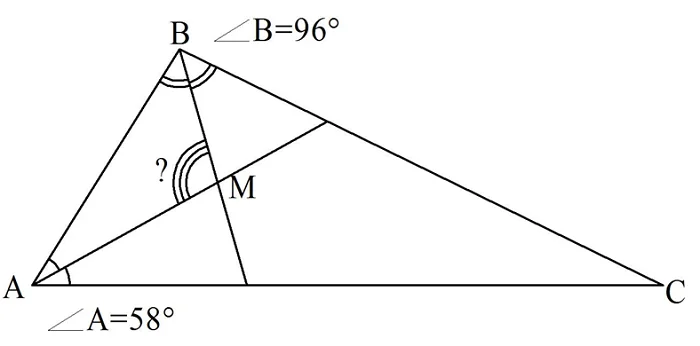
АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:

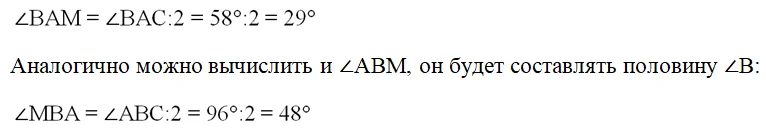
Отметим найденные углы на рисунке:

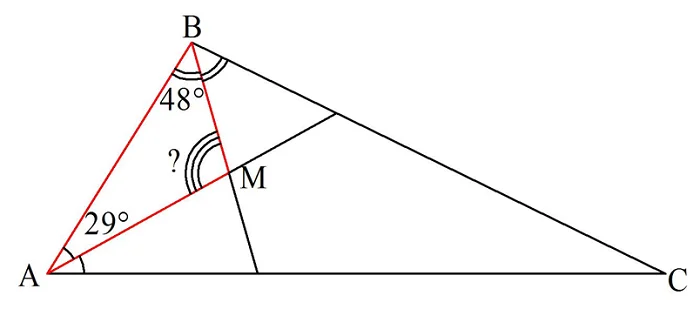
Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем

Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:

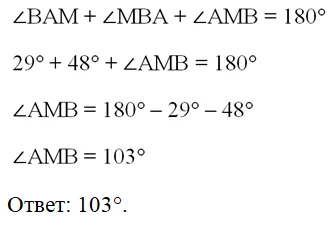
Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.

Решение. Выполним построение:

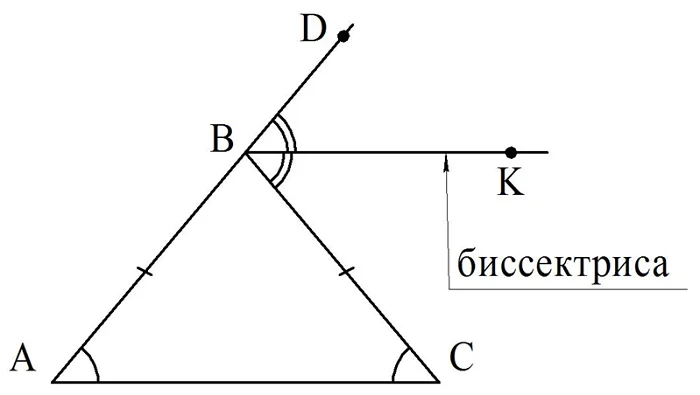
Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.

Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть

В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.

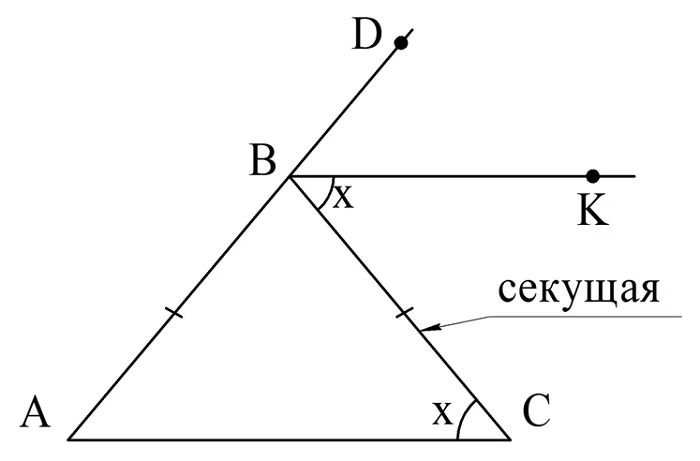
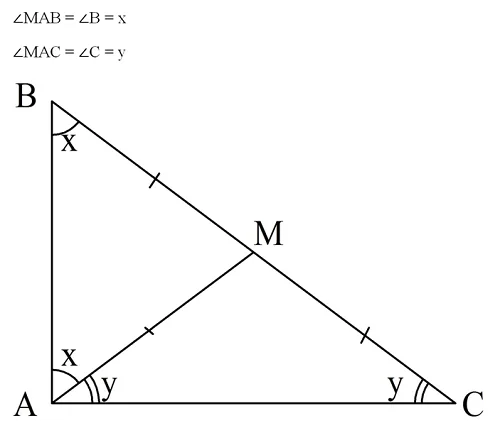
Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.

Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:

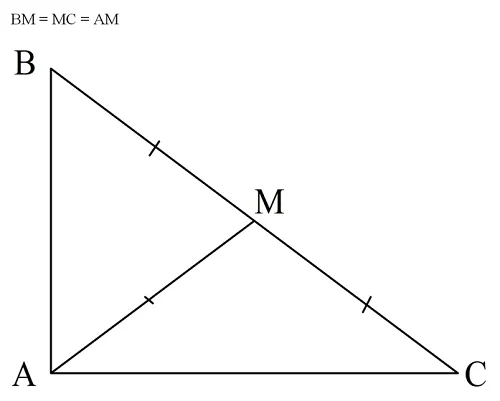
Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому

Типы треугольников

Типы треугольников
Остроугольный	Тупоугольный	Прямоугольный
Разносторонний	Равнобедренный	Равносторонний

По величине углов

сумма углов треугольника равна 180°.

Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми(меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

• Разносторонним (неравносторонним) называется треугольник, у которого все три стороны не равны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота,медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Неравенство треугольника

Следующая важная теорема называется неравенством треугольника:

Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:

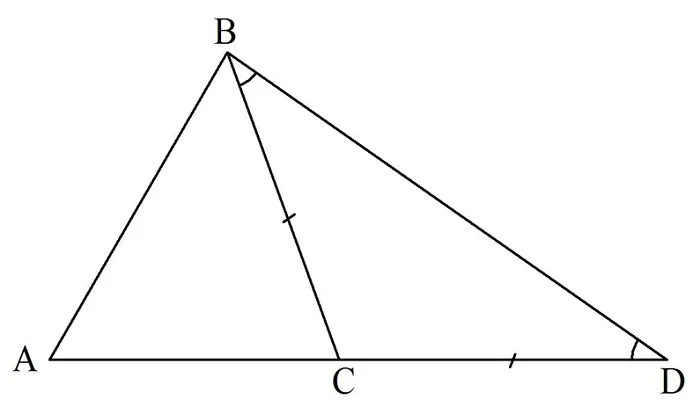
Так как AD = АС + СD, то нам достаточно показать, что АВ <AD. Ясно, что ∆ВСD является рав-бедр., ведь ВС = СD. Это значит, что

Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.

Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:

7 > 2 + 3

Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.

Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?

Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.

Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:

Треугольники

Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.

Стороны треугольника

Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам.

Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник. В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Теоремы равнобедренных треугольников: 1) углы при основании равны, 2) если в треугольнике два угла равны, то это равнобедренный треугольник, 3) медиана, которая проведена к основанию, является биссектрисой и высотой.

Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.

Углы треугольника

Треугольники бывают остроугольными, тупоугольными и прямоугольными.

Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.

Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.

Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.