Алгебра

Аксиомы теории вероятностей

Из статистического определения вероятности случайного
события следует, что вероятность события есть число, около которого
группируются частоты этого события, наблюдаемые на опыте. Поэтому
аксиомы теории вероятностей вводятся так, чтобы вероятность события
обладала основными свойствами частоты.

Аксиома 1.Каждому
событиюсоответствует
определенное число,
удовлетворяющее условиюи
называемое его вероятностью.

Аксиома 2.Вероятность
достоверного события равна единице.

Аксиома 3.Вероятность
невозможного события равна нулю.

Аксиома 4.(аксиома
сложения). Вероятность суммы двух несовместных событий равна сумме
их вероятностей.

Теория вероятностей: определение, зачем нужна

Теорию вероятностей изучают на уроках алгебры в 9 классе. 

Для чего нужно знать теорию вероятностей

Базы теории вероятностей необходимо знать каждому для того, чтобы сформировать правильное мировоззрение, для понимания того, что люди живут в вероятностном, случайном мире, в котором происходят самые случайные события, а закономерности проявляются через тысячи случайностей.

Чем сложнее система, тем намного труднее найти закономерности. В данных случаях пользуются вероятностными методиками. Так получается, что теория вероятности крайне актуальна в современном мире как в точных науках, математике, так и в обычной жизни.

Что изучает теория вероятностей

Базовыми объектами теории вероятностей являются случайные величины, события, процессы, то есть практически весь мир вокруг человека.

События бывают невозможные и достоверные. Если в процессе каждого эксперимента происходит какое-то событие, то такое событие называют достоверным. Если в процессе каждого эксперимента какое-то событие в принципе не может совершиться, то такое событие называют невозможным. Если событие не является ни достоверным, ни невозможным, то такое событие называют случайным.

Во многих сферах деятельности человека появляются ситуации, когда конкретные явления способны повторяться бесконечное число раз при одинаковых условиях. При анализе таких простых явлений, как, например, подбрасывание монетки, выброс карты, игральной кости, человек может заметить две особенности, которые присущи данным экспериментам.

1. Не представляется вероятным предсказывать результата будущего исследования по результатам предыдущих экспериментов, какое бы число исследований не было бы проведено.
2. Относительная частота конкретных результатов по мере того, как растет количество попыток, стабилизируется, медленно приближаясь к конкретному пределу.

Самое важное понятие в теории вероятности — вероятность. Данное слово, синонимом которому служит слово «шанс», часто используют в жизни

Каждый встречал фразы типа: «Сегодня, вероятно, пойдет дождь», «вероятнее всего, футбольный матч закончится вничью» и т. д. Данные фразы на уровне интуиции оценивают процент вероятности того, будет ли конкретное событие или нет. Математические вероятности придают числовую оценку тому, что может произойти.

Дискретные и непрерывные случайные величины

Случайные величины могут быть дискретными и непрерывными.

Дискретная случайная величина, это такая величина, все возможные значения которой образуют конечную или бесконечную последовательность чисел (x₁,x₂,…,x_n) и
принятие ей каждого из указанных значений есть случайное событие, характеризующееся соответствующей вероятностью (P₁,P₂,…,P_n).

При этом выполняется условие нормировки на единицу, то есть сумма всех этих вероятностей должна быть равна единице.

Непрерывная случайная величина, это такая величина, все возможные значения которой целиком заполняют некоторый промежуток и попадание в любой интервал (x₁,x₂) есть
случайное событие, характеризующееся соответствующей вероятностью P{x₁⩽x⩽x₂}.

При этом также выполняется условие нормировки на единицу, то есть вероятность достоверного события равна единице.

P{-∞⩽x⩽+∞} = 1

Генеральная совокупность, это все возможные значения, которые может принимать случайная величина.

Свойства вероятностей

Свойство 1. Если можно вычислить возможности возникновения события А и их число совпадает общим числом равновозможных событий, то вероятность события А равна 1.

Например, при бросании игральной кости число возможностей выпадения чисел 1, 2, 3, 4, 5, 6 равно 6. Насчитывается также 6 равновозможных несовместимых событий. Таким образом, M = N  и

Свойство 2. Вероятность невозможного события равна 0. Если число возможностей события А равна 0, то и

Например, при бросании игральной кости не может выпасть число 9, потому что такого числа нет на гранях игральной кости.

Свойство 3. Вероятность случайного события всегда больше 0 и меньше 1:

или

Определение статистической вероятности. В определении статистической вероятности используется понятие относительно частоты события А. Относительной частотой события А называют отношение числа наблюдений, в которых наблюдается А, к числу всех наблюдений. Относительную частоту обычно обозначают буквой W. Если в n наблюдениях событие А наблюдается m раз, то относительная частота события А:

Например, баскетболист у штрафной линии готовится совершить бросок. Из собранной тренером статистической информации известно, что у этого баскетболиста из 100 штрафных бросков успешны 70. Вероятность того, что баскетболист реализует штрафной бросок:

Длительные наблюдения показали, что с увеличением числа наблюдений относительная частота события А становится всё более стабильной. Число, около которого при серии наблюдений колеблется относительная частота, называется статистической вероятностью события А. Формула статистической вероятности события А:

если .

Вычислить точную статистическую вероятность невозможно, так как невозможно выбрать бесконечно большое число наблюдений.

Преимущество статистического определения вероятности в том, что оно не требует
априорных знаний об исследуемом объекте. Классическую вероятность можно вычислить до наблюдения или
испытания, а статистическую – после наблюдения или испытания.

Назад

Листать

Вперёд>>>

Противоположные события

Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.

Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:

0,7 + 0,3 = 1

Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.

Противоположными являются такие события, как:

• падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
• выпадение четного или нечетного числа на шестигранном кубике;
• изготовление рабочим годной или получение бракованной детали.

Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.

Очевидно, что сумма вероятностей противоположных событий равна единице.

Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?

Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице

Р(А) + Р(B) = 1

По условию Р(А) = 0,97. Тогда

0,97 + Р(В) = 1

Перенесем в равенстве слагаемое 0,97 в правую часть и получим:

Р(B) = 1 – 0,97

Р(В) = 0,03

Ответ: 0,03

Противоположные события

Два события называются противоположными при условии, что первое событие происходит всегда, когда не происходит второе, и наоборот. Проще разобраться на примерах:

• За окном идет дождь. Противоположное событие — не идет дождь;
• Студент сдал экзамен или не сдал;
• Сейчас день или ночь;
• Монета упала орлом или решкой;
• На игральном кубике выпала грань с пятеркой или не выпала грань с пятеркой;

Примеров противоположных событий много. Но тут надо быть аккуратными: события, что на кубике выпала пятерка и что выпала тройка, не будут противоположными! То, что не выпала пятерка, не означает, что обязательно выпала тройка, могла же выпасть любая грань: единица, двойка, тройка, четверка или шестерка. Противоположным событием для выпадения пятерки, будет событие выпадения любой другой грани кроме пятерки.

В примере с монетой орел и решка являются противоположными событиями, так как, если не выпал орел, то больше вариантов нет: обязательно выпала решка.

Противоположные события характеризуются отрицанием — словом «НЕ».

ТеоремаСумма вероятностей противоположных событий всегда равна единице.

Напомню, что вероятность некоторого события, равная единице, означает, что это событие точно произойдет.

Тогда доказательство этой теоремы интуитивное и следует из определения противоположных событий: если не произошло одно, то обязательно произойдет противоположное ему.

Что-то из двух противоположных событий точно произойдет, поэтому, если сложить их вероятности, то сумма будет равна единице:
$$P(A)+P(\overline A)=1;$$
где \(P(A)\) — вероятность некоторого события;
\(P(\overline A)\) — вероятность события противоположного \(A;\)

Обычно эту формулу записывают так:
$$P(\overline A)=1- P(A);$$
Чтобы найти вероятность события противоположного \(A,\) нужно из единицы вычесть вероятность события \(A.\)

Разберем на примерах:Пример 1На устном экзамене по литературе 50 вопросов, Валера выучил только 36 из них. Какая вероятность, что Валере попадется невыученный вопрос?

Статистическое определение вероятности

Формулу (1.1) используют для непосредственного
вычисления вероятностей событий только тогда, когда опыт сводится к
схеме случаев. На практике часто классическое определение
вероятности неприменимо по двум причинам: во-первых, классическое
определение вероятности предполагает, что общее число случаевдолжно
быть конечно. На самом же деле оно зачастую не ограничено.
Во-вторых, часто невозможно представить исходы опыта в виде
равновозможных и несовместных событий.

Частота появления событий при многократно повторяющихся
Опытах имеет тенденцию стабилизироваться около какой-то постоянной
величины. Таким образом, с рассматриваемым событием можно связать
некоторую постоянную величину, около которой группируются частоты и
которая является характеристикой объективной связи между комплексом
условий, при которых проводятся опыты, и событием.

Вероятностью случайного события называется число, около которого
группируются частоты этого события по мере увеличения числа
испытаний.

Это определение вероятности называетсястатистическим.

Преимущество статистического способа определения вероятности состоит в
том, что он опирается на реальный эксперимент. Однако его
существенный недостаток заключается в том, что для определения
вероятности необходимо выполнить большое число опытов, которые очень
часто связаны с материальными затратами. Статистическое определение
вероятности события хотя и достаточно полно раскрывает содержание
этого понятия, но не дает возможности фактического вычисления
вероятности.

Операции над событиями

При разработке аппарата и методики исследования случайных событий в
теории вероятностей очень важным является понятие суммы и
произведения событий.

Суммой, или объединением, нескольких событий
называется событие, состоящее в наступлении хотя бы одного из этих
событий.

Суммасобытийобозначается
так:

.

Например, если событиеесть
попадание в цель при первом выстреле, событие—
при втором, то событиеесть
попадание в цель вообще, безразлично, при каком выстреле — первом,
втором или при обоих вместе.

Произведением, или пересечением, нескольких событий
называется событие, состоящее в совместном появлении всех этих
событий.

Произведениесобытийобозначается

.

Например, если событиеесть
попадание в цель при первом выстреле, событие—
при втором, то событиесостоит
в том, что в цель попали при обоих выстрелах.

Понятия суммы и произведения событий имеют наглядную
геометрическую интерпретацию. Пусть событиесостоит
в попадании точки в область,
событие—
в попадании в область,
тогда событиесостоит
в попадании точки в область, заштрихованную на рис. 1, и событие—
в попадании точки в область, заштрихованную на рис. 2.

Кто придумал теорию вероятностей

Основателями теории вероятностей являются два французских математика Блез Паскаль и Пьер Ферма. В 1654 г. французский писатель Антуан Гомбо (известный как Шевалье де Мере), интересовавшийся игрой и азартными играми, вызвал заинтересованность Паскаля насчёт популярной в то время игры в кости.

Кости бросались 24 раза, а вопрос стоял в том, стоит ли ставить деньги на выпадение хотя бы одной «двойной шестёрки». В то время считалось, что это было выгодно, но последующие расчёты показали прямо противоположное.

Узнайте про Метод Крамера, Интегралы, Корреляции, Математическое ожидание, Стандартное отклонение и Космологию.

Виды событий

В теории вероятностей события бывают невозможными, случайными и достоверными.

Невозможное событие

Это то, которое уже известно, что в ходе испытания НЕ произойдёт, т. е. вероятность данного события равна нулю. Например: при бросании одной игральной кости (один раз), какова вероятность того, что выпадет 7 очков?

Случайное событие

Это событие может произойти или нет, обычно оно именно случайное. Например: при бросании игральной кости, какова вероятность того, что выпадет чётное число очков?

Достоверное событие

Это то, которое в ходе испытания обязательно произойдёт, т. е. вероятность данного события равна 1. Например: при бросании игральной кости, какова вероятность того, что она не останется в воздухе, а упадёт?

Вероятность и случайная величина

Вероятность, это количественная мера наступления какого-нибудь случайного события.

Вероятность является первичным базовым понятием в математике, и ее нельзя определить через более простые термины и понятия.

Случайная величина, это такая величина, которая принимает те или иные значения с определенными вероятностями.

Вероятность может принимать значение от нуля до единицы (0⩽P⩽1). Ноль означает невозможное событие (P=0). Единица означает достоверное событие, которое обязательно случится
(P=1).

Например, Вы держите в руке тяжелую гирю и выпускаете её из рук. С вероятностью P=1 гиря упадет вниз. С вероятностью P=0 гиря зависнет в воздухе как в невесомости.

Еще пример. Вы подбрасываете 6-гранный кубик с пронумерованными гранями. Два очка выпадет с вероятностью P=1/6, то есть примерно в каждом шестом испытании. Пять очков тоже выпадет с вероятностью
P=1/6, то есть тоже в каждом шестом испытании.

А теперь более хитрый пример. Вы подбрасываете монету. Вероятность выпадения решки равна вероятности выпадения орла. И та и другая вероятность равна половине (P=1/2).

А может ли монета после подбрасывания встать вертикально на ребро? В прошлом примере мы считали, что это невозможное событие, то есть вероятность такого события P=0. Однако, теоретически такое
случайное событие может произойти. Но вероятность такого случайного события очень-очень маленькая. Возможно, более вероятно, что Вам на голову когда-нибудь упадет метеорит, чем Вы увидите, как после
подбрасывания, монета встала на своё ребро.

Пусть вероятность того, что монета встанет на своё ребро будет P=0.0000002. (Это на самом деле не так, это число взято только для примера.) Чему тогда равна вероятность выпадения орла?

Эта вероятность уже не будет равной P=0.5, так как сумма вероятности всех возможных событий не может быть равной чему-то больше единицы. В самом деле, если мы подбрасываем монету, то или выпадет
решка или выпадет орел или она встанет на ребро. Ничего другого не случится. Значит, вероятность выпадения решки или орла или ребра будет равна единице (P=1). Достоверно произойдет одно из трех
событий.

Поэтому, в силу симметрии между решкой и орлом, получаем, что вероятность выпадения орла будет P=0.4999999. И такая же будет вероятность выпадения решки.

0.4999999 + 0.4999999 + 0.0000002 = 1.

А если монета не может становиться на ребро, то

0.5 + 0.5 = 1.

Для 6-гранного кубика вероятность выпадения каждой из его граней P=1/6. Значит, вероятность того, что выпадет хотя бы одна грань (а это достоверное событие, которое обязательно произойдет) будет

1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Вероятность и геометрия

Теория вероятности затрагивает и геометрию. Пусть есть отрезок АВ, в середине которого располагается точка С.

Теперь мы ставим на отрезке АВ случайную точку D. С какой вероятностью она попадет наАС, а с какой на ВС? Так как эти отрезки ничем не отличаются, то можно предположить, что события «попадание точки на АС» и «попадание точки на ВС» являются равновероятными событиями. Так и есть. Их вероятность обоих событий составляет 0,5.

Теперь предположим, что точка С выбрана так, что отрезок АС вдвое короче, чем ВС, то есть ВС = 2 АС:

Чему в этом случае равны вероятности попадания случайной точки D на отрезки АС и ВС? Для ответа на этот вопрос раздели ВС надвое с помощью ещё одной точки K:

Получили три одинаковых отрезка АС, СК и КВ. Раз они одинаковы, то и вероятности случайной точки оказаться на каждом из этих отрезков равны:

Р(АС) = Р(СК) = Р(КВ) = 1/3

Отсюда вероятность попадания точки на ВС равна 2/3:

Р(ВС) = Р(СК) + Р(КВ) = 1/3 + 1/3 =2/3

Получили, что вероятность попадания точки на ВС вдвое выше, чем на АС. И при этом ВС вдвое длиннее. И это не случайно. В общем случае верно следующее правило:

Данное свойство может пригодиться не только в геометрии, но и при решении задач.

Пример. Прохожий пришел на остановку автобуса в случайный момент времени. Он знает, что автобус ходит с интервалом в 40 минут, но не знает, когда отъехал предыдущий автобус. С какой вероятностью автобус придется ждать менее 10 минут?

Решение. Построим схему. На ней время будем откладывать по горизонтальной оси. Отметим точки, соответствующие приезду автобуса (А₁, А₂, А₃, А₄), и точку, соответствующую приходу прохожего (D):

Ясно, что точка D окажется между какими-то двумя точками, которым соответствуют последовательные прибытия поезда.На рисунке это А₂ и А₃. В каком случае время ожидания составить менее 10 минут? В том случае, если точка D окажется на «расстоянии» менее 10 минут от точки А₃, то есть попадет в отрезок ВА₃:

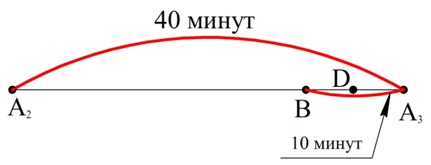
Отрезок ВА₃ вчетверо короче отрезка А₂А₃, поэтому вероятность точку D попасть на него составляет 1/4. Именно такова вероятность, что прохожему придется ждать автобус менее 10 минут.

Ответ: 1/4

В случае, когда точка случайным образом ставится не на отрезке, а на плоской фигуре, то справедливо следующее правило:

Пример. В треугольнике АВС проведена средняя линия NM. С какой вероятностью случайная точка, отмеченная на треугольнике АВС, попадет и на треугольник ANM?

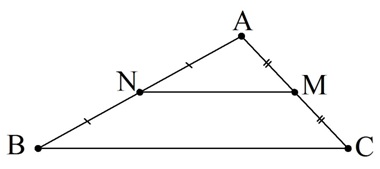
Решение. Средняя линия NM параллельна стороне ВС (это свойство средней линии), а потому равны углы АNM и АВС (соответственные углы при параллельных прямых). Это значит, что треугольники АВС и ANM подобны по двум равным углам. Коэффициент подобия равен 1/2, так как AN/АВ = 1/2. Известно, что отношение площадей подобных фигур равно квадрату их коэффициента подобия, поэтому площадь АMN в 4 раза меньше площади АВМ. По условию точка гарантированно попадает в АВС, то есть вероятность этого события равна 1. Тогда вероятность попадания точки в АNM будет в 4 раза меньше и составит 1/4 .

Ответ:1/4.

Элементарные события

Часто одно случайное событие можно представить как результат нескольких случайных событий. Например, событие «выпадение на кубике четного числа» произойдет в том случае, если случится хотя бы одно из следующих событий:

• выпадет двойка;
• выпадет четверка;
• выпадет шестерка.

Если событие нельзя «разбить» на более простые события, то его называют элементарным событием. Считается, что в ходе испытания может произойти только одно элементарное событие. Так, при броске кубика произойдет одно из 6 элементарных событий:

• выпадет единица;
• выпадет двойка;
• выпадет тройка;
• выпадет четверка;
• выпадет пятерка;
• выпадет шестерка.

В большинстве случаев вероятность элементарных событий одинакова. Действительно, нет причин полагать, что при броске кубика шестерка будет выпадать чаще двойки. Если у двух элементарных событий одинаковая вероятность, то их называют равновозможными событиями.

Если в результате эксперимента происходит одно из равновозможных событий, число которых равно n, то вероятность каждого из них принимается равной дроби 1/n.

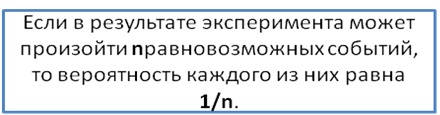
Например, при броске кубика может произойти 6 равновозможных событий. Значит, вероятность каждого из них равна 1/6. При броске монетки она может выпасть либо орел, либо решка. Этих событий два, и они равновозможны, поэтому их вероятность равна 1/2, то есть 0,5.

Пример. В урне 20 шариков, один из которых окрашен в желтый цвет. Какова вероятность, что человек, вытаскивающий вслепую один из шариков, вынет именно желтый шар?

Решение. Так как шаров 20, то возможны 20 равновозможных событий, одно из которых – вытаскивание желтого шара. Его вероятность равна 1/20 = 0,05

Ответ: 0,05

Пример. Вася составил произвольную последовательность из букв А, Б, В, Г, Д, и записал ее на бумаге. Каждую букву Вася использовал один раз. Аналогично свою последовательность записал и Петя. Какова вероятность, что они оба загадали одну и ту же последовательность.

Решение. Вася записал перестановку 5 букв. Общее количество таких перестановок равно 5! = 1•2•3•4•5 = 120. Все последовательности равновероятны. Значит, вероятность того, что они совпали, равна 1/120.

Ответ: 1/120

Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности

Операция сложения вероятностей будет означать связку «или», операция умножения вероятностей будет означать связку «и».

Сложение вероятностей

Сумма двух событий A и B будут называть событие A+B. Оно состоит в том, что может наступить или событие B, или событие A, или же оба события в одно и то же время. Если же события являются несовместимыми, последний вариант невозможен, таким образом возможно наступление или события B, или события A.  

Умножение вероятностей

Произведение двух вероятностей A и B — событие AB, оно состоит в том, что события проявляются совместно. Другими словами, умножение AB будет следующим: в результате некоторых условий может наступить и событие A, и событие B. Это утверждение является справедливым для большого числа событий. Так, например, произведение  предусматривают, что в конкретных условиях может произойти и событие , и событие и событие  , и событие .

Так получается, что событие  будет состоять в том, что на монетах (и на первой, и на второй) выпадает орел.

Событие — на монетах выпадает решка (и на первой, и на второй).

Событие  — на первой монете будет орел, а на второй монете будет решка.

Событие — на первой монете будет решка, а на второй монете будет орел.

Полная группа событий

Зависимое событие A способно произойти только в итоге реализации одной из несовместимых гипотез  до бесконечности, они образуют полную группу событий. Пусть будут известны вероятности событий , а также соответствующие условные вероятности .

Приведенная выше формула является формулой полной вероятности.

В учебниках алгебры она формулируется при помощи теоремы, которую можно доказать очень просто: по алгебре событий  (случилось событие  и после него случилось событие A или случилось событие  и после него случилось событие A и так до бесконечности).

Из-за того, что гипотезы  и до бесконечности являются несовместимыми, а событие A является зависимым, то по теореме сложения вероятностей несовместимых событий и теореме умножения вероятностей зависимых событий: 

Объединение и пересечение событий

Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим? 

Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий. 

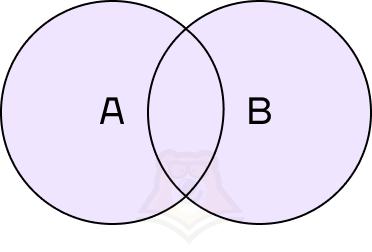
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег. 

Объединение событий обозначается знаком \(\cup\). Объединение событий А и В можно записать как \(A \cup B\). 

Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?

Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям. 

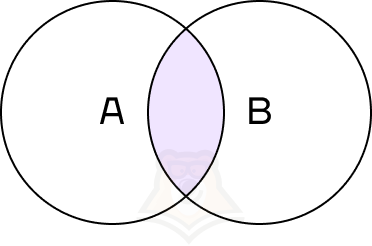
Пересечение событий обозначается знаком \(\cap\). Пересечение событий А и В можно записать как \(A \cap B\). 

Проверь себя

Задание 1. Какие события являются несовместными?

1. Подбрасывание монетки.
2. Брак батареек в одной упаковке.
3. “Миша идет” и “Миша стоит”.
4. Случайное вытаскивание конфет из вазы. 

Задание 2. Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

1. 0,17
2. 1
3. 0,83
4. 1,17 

Задание 3. Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1. 1
2. 0,216
3. 0,45
4. 1,5 

Задание 4. В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут. 

1. 0,3
2. 0,001
3. 2,7
4. 0,729 

Задание 5. Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой. 

1. 0,77
2. 0,135
3. 0,23
4. -0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться. 

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов. 

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат. 

Как кот может быть одновременно жив и мертв? Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом. По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив. Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным.  Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

• выпадет орел;
• выпадет решка. 

Эти два события образуют множество элементарных событий. 

Множество элементарных событий — множество всех возможных результатов случайного эксперимента. 

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации. 

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран. 

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности. 

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу. 

\(P = \frac{m}{n}\)

Вероятность можно обозначить, как P(x), где х — некоторое событие. 

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Можно ли всегда выигрывать спор с монеткой?Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна \(P = \frac{2}{2} = 1\), то есть мы точно выиграем спор. Однако вероятность не так проста, и даже здесь подготовила ловушку. В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет  \(\frac{1}{6000}\). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%. 

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна \(\frac{49}{140} = 0,35\)

Выразим в процентах:  0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ. 

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой. 

\(P = \frac{m}{n} * 100%\)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.