Таблицы и операции
Построить таблицу истинности можно без онлайн калькуляторов. Для этого достаточно запомнить, как работает каждая из перечисленных выше операций. У математиков с этим проблем не возникает – они хорошо заучивают предложенную далее информацию.
Конъюнкция
Носит название «логическое И» или «умножение». Часто встречается в программировании. В языках «создания контента» обладает особым обозначением. Примеры записи:
- И;
- AND;
- &;
- &&.
Выражение логического характера при конъюнкции является истиной, только когда оба простых высказывания тоже выступают в качестве правды. Если хотя бы одно из них – ложь, то вся операция примет значение False.
Выше представлена таблица истинности при операции конъюнкции.
Дизъюнкция
Является сложением. У этого логического выражения есть иное название – «логическое ИЛИ». Тоже встречается в программировании довольно часто.
Может иметь такие формы записи:
- ||;
- ИЛИ;
- OR;
- |.
Преобразование последовательности будет осуществляться по принципу: выражение – истина, если хотя бы одно из его составляющих – правда. Ложно, когда оба элемента имеют значение FALSE.
Выше – примеры таблицы истинности, которая работает в отношении дизъюнкции.
Инверсия
Следующий момент, на который стоит обратить внимание – это инверсия. Носит название «отрицание» или «логическое НЕ»
Обозначения в программировании:
- НЕ;
- !;
- NOT.
Логическое выражение при отрицании обладает следующими особенностями:
- Когда исходные данные истины, то результатом станет ложь.
- Если операция обладает значением «ложь», ее отрицание получит «истину».
- Можно рассматривать соответствующую манипуляцию как трактовку «Неверно, что…»
Вот такую таблицу истинности можно построить относительно инверсии.
Импликация
При любом логическом выводе стоит опираться на предлагаемые примеры и таблицы. Импликация – это следование.
В любом заданном логическом выражении результат – это истина всегда. Исключение – когда из правды следует ложь. Она связывает два высказывания (a и b), где:
- A – это условие, первое выражение;
- B – следствие.
Если из A может следовать B, значит операция выдаст в результате обработки «истину».
Эквивалентность
Так называют равнозначность. Новое высказывание истинно тогда, когда оба простых выражения – это правда.
Выше – пример расчетов формулы логики заданных высказываний при эквивалентности.
Исключение
Онлайн калькуляторы могут помочь построить график или указать, что верно, а что нет, без вдумчивости в поставленную задачу со стороны пользователя. Но программистам приходится прописывать принципы функционирования и выполняемые операции вручную. Для них особенности алгебры логики и информатики крайне важны.
Порядок выполнения логических операций ранее был рассмотрен. Осталось понять, как работает исключение.
Согласно установленным правилам, операция будет истиной, когда среди значений переменных A и B есть одно правдивое. Если оба – это действительность, упомянутый принцип работать не будет.
Исключающее ИЛИ – преобразование, которое носит название «сложение по модулю два».
Метод таблиц
Основным приемом для решения текстовых логических задач является метод таблиц. С помощью таблиц можно наглядно представить условие задачи или ее ответ, кроме того их использование значительно помогают в принятии правильных логических решений.
Пример 2
У трех кукол Маши, Даши и Алены были платья трех разных цветов: красного, зеленого и синего. Туфли у них были таких же цветов. У Маши цвет платья и туфель совпадали. У Алены ни туфли, ни платье не были красными. Даша была в зеленых туфлях и в платье другого цвета. Как были одеты куклы?
Решение:
Составим таблицу, в которой отметим возможные цвета платьев и туфель кукол. По условию задачи заполним таблицу:
-
туфли Даши зеленые, а платье не зеленое. Следовательно, у Маши и Алены туфли уже не могут быть зелеными, так же как не могут быть туфли Даши синими или красными. Отмечаем все в таблице:
-
туфли и платье Алены не являются красными. Из таблицы видим, что красные туфли могут быть только у Маши, а, следовательно, туфли Алены — синие. Правая часть таблицы заполнена.
 Рисунок 1.
Рисунок 1.
Цвет платья Маши совпадает с цветом ее туфель, значит оно красное. Теперь легко увидеть, что у Алены — зеленое платье, а у Даши — синее.
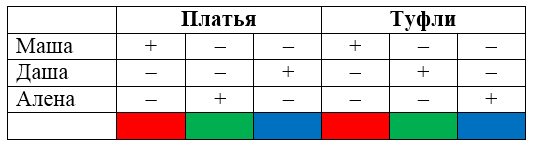 Рисунок 2.
Рисунок 2.
Таблица полностью заполнена и в ней однозначно установлены цвета туфель и платьев кукол.
Ответ: Маша одета в красное платье и красные туфли, Даша в синем платье и зеленых туфлях, Алена в зеленом платье и синих туфлях.
Метод блок-схем
Этим методом решаются задачи, в которых с помощью сосудов требуется отмерить необходимое количество жидкости или связанные со взвешиванием на чашечных весах. Простейшим приемом решения таких задач является перебор всех возможных вариантов, который не является удобным и не дает возможности выделения общего подхода к решению подобных задач.
Суть метода блок-схем состоит в следующем:
- выделяют операции для точного отмеривания жидкости, которые называются командами;
- устанавливают последовательность выполнения команд, которая оформляется в виде блок-схемы (как в программировании). Составленная блок-схема является программой, выполнение которой должно привести к решению задачи, в ходе которой достаточно отмечать получаемые количества жидкости.
При выполнении программы удобно заполнять отдельную таблицу, в которую заносится количество жидкости в каждом из имеющихся сосудов.
Законы алгебры логики
В логике высказываний известно много общезначимых формул, которые также называются законами логики
высказываний. Основными законами являются следующие:
- законы идемпотентности (повторение действия над объектом не изменяет его, латинский idem — «тот же
самый»
и potens — «способный»):- $x \land x = x$
- $x \lor x = x$
- $x \land 1 = x$ — $x$ и Истина всегда будет $x$
- $x \lor 1 = 1$ — $x$ или Истина всегда будет Истина
- $x \land 0 = 0$
- $x \lor 0 = x$
- $x \land \lnot x = 0$ – закон противоречия
- $x \lor \lnot x = 1$ – закон исключения третьего
- $\lnot \lnot x = x$ – закон снятия двойного отрицания
- законы поглощения
- $x \land (y \lor x) = x$
- $x \lor (y \land x) = x$
Доказать эти и последующие законы можно с помощью построения таблиц истинности или
простейших логических рассуждений.
Следующая группа законов представляет взаимосвязь между логическими операциями:
- $(x \equiv y) = (x \Rightarrow y) \land (y \Rightarrow x)$
- $x \Rightarrow y = \lnot x \lor y$
- законы Де Моргана
- $\lnot(y \lor x) = \lnot y \land \lnot x$
- $\lnot(y \land x) = \lnot y \lor \lnot x$
Замечательным следствием приведенных выше законов является следующий факт. Любую логическую формулу можно заменить
равносильной ей, но содержащую только две логические операции:
- конъюнкцию «и» и отрицание «не»
- дизъюнкцию «или» и отрицание «не»
Дальнейшее исключение логических операций, очевидно, невозможно, то есть приведенные пары представляют минимальный
базис для построения правильно построенных формул. Однако существует операция, с помощью которой можно представить
любую логическую связку. Эта операция получила название «штрих Шеффера» и определяется следующим образом:
| $x$ | $y$ | $x | y$ |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
На основании этого определения можно ввести следующие законы, выражающие взаимосвязь операции «штрих Шеффера» и
других логических связок:
- $\lnot x = x | x$ — связка «не» через «штрих Шеффера»
- $x \land y = (x | y) | (x | y)$ — связка «и» через «штрих Шеффера»
Также следует отметить, что $x | y= \lnot (x \lor y)$.
К основным законам алгебры логики также относятся следующие:
- коммутативные законы (от перестановки мест результат не меняется)
- $x \land y = y \land x$
- $х \lor y = y \lor x$
- дистрибутивные законы (правила группировки)
- $x \land (y \lor z) = (x \land y) \lor (x \land z)$
- $x \lor (y \land z) = (x \lor y) \land (x \lor z)$
- ассоциативные законы
- $x \land (y \land z) = (x \land y) \land z$
- $x \lor (y \lor z) = (х \lor y) \lor z$
С помощью законов логики можно осуществлять равносильные преобразования. Такие преобразования используются для
доказательств, приведения формул к заданному виду, упрощения формул.
Под сложностью формул обычно понимается количество символов, используемых для ее записи. То есть формула $\alpha$
проще
формулы $\beta$, если $\alpha$ содержит меньше букв и логических операций. Например, для формулы
$(\lnot (x \lor y) \Rightarrow x \lor y) \land y$
можно записать следующую цепочку преобразований, приводящих ее к более простому виду:
$(\lnot \lnot(x \lor y) \lor x \lor y) \land y = (x \lor y \lor x \lor y) \land y = (x \lor y) \land y = y$.
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором

Рассмотрим все варианты:
- Все контакты включены, тогда источник света горит.
- Первый контакт в положении «выключено» – свет не горит.
- Второй контакт выключен – лампа не светит.
- Все контакты отключены – свет не горит.
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
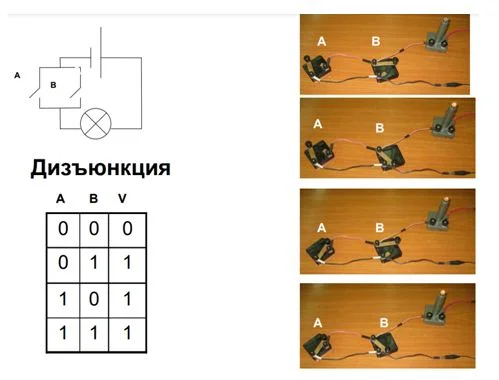
Рассмотрим этот вид электрической цепочки:
- Все контакты включены – лампа горит.
- Первый контакт включен, второй выключен – свет горит.
- Обратная ситуация – выключен первый, включен второй – лампа светится.
- Все контакты выключены – света нет.
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
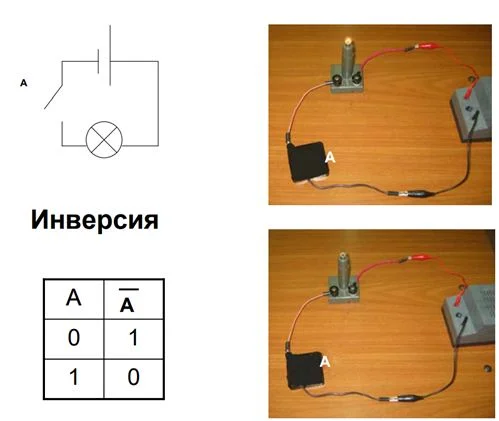
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
Высказывание и операции над высказыванием
Исходным (базовым) понятием является простое высказывание.
Под высказыванием обычно понимают всякое предположение, утверждающее что-либо о чем-либо. Если смысл,
содержащийся в высказывании, соответствует
действительности, то высказывание является истинным, иначе
ложным.
Обычно элементарные высказывания обозначают строчными буквами латинского алфавита $a$, $b$, $c$,
$x$, $y$ …, которые являются логическими переменными в логических формулах. Истинные
значения обозначаются
буквой И (True, T) или 1, а ложные – Л (False, F) или 0.
Бинарные функции
$n = 2$ — количество аргументов.
$k_n = 2^2 = 4$
$k_ф = 2^4 = 16$
| $x$ | $y$ | $f_0$ | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ | $f_{10}$ | $f_{11}$ | $f_{12}$ | $f_{13}$ | $f_{14}$ | $f_{15}$ |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| const «0» | $x \land y$ | пер. $x$ | пер. $y$ | $x \xor y$ | $x \lor y$ | const «1» |
Номер функции совпадает с двоичной записью функции
- $f_1$ — коньюнкция. $x \& y$ — $x$ и $y$ — ${x} and {y}$ $x \&\& y$
- $f_7$ — дизъюнкция. $x | y$ — $x$ или $y$
- $f_{11}$ и $f_{13}$ — импликация (следование)
- $f_9$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
- $f_6$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
Из элементарных высказываний можно составить более сложные с помощью логических связок:
- $\lnot$ — логическое «не» (отрицание)
- $\land$ — логическое «и» (конъюнкция) — «и одновременно»
- $\lor$ — логическое «или» (дизъюнкция)
- $\Rightarrow$ — «логическое следствие» (импликация)
- $\equiv$ — «эквивалентность»
- круглых скобок (, ) — групировка операций.
- …есть и другие (менее распространённые) связки…
Логические связки
можно определить с помощью таблицы истинности. В левой части этой таблицы перечисляются
все
возможные
комбинации значений логических переменных $x$ и $y$. В правой части – соответствующие им им значения выражений из
переменных и логических связок.
| $x$ | $y$ | $\lnot x$ | $x \land y$ | $x \lor y$ | $x \Rightarrow y$ | $x \equiv y$ |
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 |
Связки имеют следующий приоритет: $\lnot \land \lor \Rightarrow \equiv$ (приоритет можно изменить с помощью скобок).
Высказывания (формулы) из простых высказываний, связок и скобок, называют правильно построенными формулами
или просто формулами.
Значение логических связок близко к соответствующим высказываниям на
естественном языке. Например смысл связок $\lnot$ и $\land$ практически
совпадает со смыслом слов «не» и «и». Однако имеются и некоторые различия. Так формула
$x \lor y$ несколько шире, чем русское «$x$ или $y$».
Выражение «$x$ или $y$» по смыслу это формула $x \land \lnot y \lor \lnot x \land y$ (исключающее или). Еще больше
различий между семантикой
формулы $x \Rightarrow y$ в логике высказываний и выражению «из $x$ следует $y$». В русском языке это выражение
истинно, если истинны $x$ и $y$, т.е. предложение русского языка по смыслу совпадает с формулой $x \land y$.
Логическое следствие истинно также, если $x$ и
$y$ ложны или $x$ ложна, а $y$ истинна. Логическую формулу $x \Rightarrow y$ следует
интерпретировать на естественном языке так: «Если $x$ истинна, то $y$ тоже истинна, а остальное
неизвестно».
Таблица истинности — таблица в которой в левой части перечислены все возможные значения переменных, а в правой
части значения функции. Для построения таблицы истинности выписываются все возможные значения аргументов, а потом
поэтапно вычисляем значения.
Для любой формулы также можно написать таблицу истинности. Например:
| $x$ | $y$ | $\lnot x$ | $\lnot y \lor y$ | $\lnot x \land (\lnot y \lor y)$ | $\lnot x \land (\lnot y \lor y) \Rightarrow \lnot x$ |
| 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | ||||
| 1 | 1 | 1 |
Если формула содержит $n$ переменных, то в таблице истинности будет $2^n$
строк (в примере формула содержит 2 переменные и $2^2 = 4$ строки). Кроме того, данная формула истинна на
любом наборе значений своих переменных (везде 1). Такие формулы называются тождественно истинными или
тавтологиями. В противоположной ситуации, формула является тождественно ложной или
невыполнимой. Если две разные формулы принимают одинаковые значения на любом наборе значений переменных, то
такие формулы называют равносильными. Равносильные формулы обозначаются знаком равенства =.
Таблицы истинности
Например, для выражения: A ∧ (B ∨ C) ≡ B ⇒ ¬A.
Важно, чтобы порядок операций был правильным. Как всегда, сначала выполняется операция, указанная в скобках, а затем в порядке старшинства
Порядок действий следующий:
Мы создаем таблицу, в которую сразу записываем все суммы 0 и 1 для переменных A и B и добавляем столбцы для каждого шага вычислений.
Чтобы было легче записывать предложения, пронумеруйте их по порядку, начиная с 0. Переведите их количество в 2 кубика и запишите сумму чисел. У нас есть 3 различные переменные, поэтому должно быть 8 предложений.
инверсия берет только 1 переменную и сразу меняет ее значение:
конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:
дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:
эквиваленция вернет 1, если переменные равны, и 0 в противном случае:
импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:
| Последний столбец — это результат таблицы истинности. Отсюда видно, что общее исходное выражение равно 1, когда A = 1, B = 0 и C = 1, и что оно равно 0 во всех остальных случаях. |
Их не так уж мало: от самых простых и очевидных до самых сложных; от очень распространенных до очень редких.
Вам не обязательно знать их все наизусть — некоторые из них очень просты и напоминают правила математики начальной школы. Остальные стоит запомнить: если вы видите очень большое логическое уравнение, есть большая вероятность, что эти законы помогут его уменьшить.
Попробуем упростить исходное выражение ¬(¬A ∧ ¬B) ∨ B ∧ C:
¬(¬A ∧ ¬Γ) ∨ В ∧ Γ = ¬(¬A) ∨ ¬(¬Γ) ∨ В ∧ Γ
¬(A) ∨ ¬(C) ∨ В ∧ S = A ∨ В ∨ В ∧ S
A ∨ IN ∨ IN ∧ C = A ∨ IN
- Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.
- Третье действие — умножение значения А на результат первого действия:
- Четвертое — импликация значения В и результата второго действия:
- И последнее действие — эквиваленция результатов 3 и 4 действий:
В итоге нам удалось преобразовать уравнение с 3 переменными и несколькими отрицаниями в максимально простую нотацию, где осталось только 2 переменные:
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Формульно-словесный способ
При использовании формульно-словесного способа инструкции задаются более чётко. Этот тот случай, когда словесные пояснения сопровождаются перечнем конкретных действий, плюс эти пояснения характеризуются наличием формальных символов и выражений (формул).
Для примера составим формульно-словесный алгоритм вычисления выражения: z=2∙x–(y+6):
• вводим значения х и y;
• находим сумму (y+6);
• находим произведение (2∙x);
• вычисляем z как разность уже полученных выше значений: z=2∙x–(y+6);
• выводим z как результат вычисления выражения.
Это более компактный и лаконичный метод, он нагляднее, но всё же строго формальным не является.
Метод рассуждений
Метод рассуждений является самым примитивным способом и его обычно применяют для решения самых простых логических задач. Идея метода заключается в проведении рассуждений при последовательном использовании всех условий задачи, вследствие чего приходят к выводу, который является ответом задачи.
Готовые работы на аналогичную тему
- Курсовая работа Решение логических задач 460 руб.
- Реферат Решение логических задач 240 руб.
- Контрольная работа Решение логических задач 240 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость Пример 1
Владимир, Семен и Олег изучают разные иностранные языки: английский, французский и немецкий. На вопрос, какой язык изучает каждый из них, один ответил: «Владимир изучает английский, Семен не изучает английский, а Олег не изучает немецкий». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из студентов?
Решение:
Имеем три утверждения. Если принять за истину первое утверждение, то правдиво и второе, т.к. студенты изучают разные языки, что противоречит условию задачи. Таким образом первое утверждение ложно.
Если правдивым является второе утверждение, то первое и третье должны быть ложными. В таком случае получаем, что никто не изучает английский. Это противоречит условию, таким образом, второе утверждение также является ложным.
Остается третье утверждение, которое можем считать верным, а первое и второе — ложными. Таким образом, Владимир не изучает английский, его изучает Семен.
Ответ: Семен изучает английский язык, Олег — французский, Владимир — немецкий.
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут!
Задать вопрос
Виды выражений
С помощью логических операций можно строить теории, а также решать сложные задачи, результатом которых окажется справедливый итог. Стоит помнить о том, что прослеживать имеющиеся связи для анализа необходимо крайне внимательно. А еще – учитывать заданные условия, которые относятся к поставленной задаче.
Логические выражения могут быть:
- простыми;
- сложными.
В первом случае результатом обработки заданной операции выступать только «истина» или «ложь». Во втором – или итогом становятся или только истинные операции, или исключительно ложные.
Процедуры получения сложного выражения из нескольких простых имеют определенное название. А именно – формулы логического характера.
Логические задачи для учеников 10, 11 классов
Задача 1.
Имеется 19 гирек весом 1 г, 2 г, 3 г, …, 19 г. Девять из них – железные, девять – бронзовые и одна – золотая. Известно, что общий вес всех железных гирек на 90 г больше, чем общий вес бронзовых. Найдите вес золотой гирьки.
Задача 2.
За круглым столом были приготовлены 12 мест для жюри с указанием имени на каждом месте. Николай Николаевич, пришедший первым, по рассеянности сел не на свое, а на следующее по часовой стрелке место. Каждый член жюри, подходивший к столу после этого, занимал свое место или, если оно уже было занято, шел вокруг стола по часовой стрелке и садился на первое свободное место. Возникшее расположение членов жюри зависит от того, в каком порядке они подходили к столу. Сколько может возникнуть различных способов рассадки жюри?
Задача 3.
В некотором государстве, в котором всего 10 городов, включая столицу, сеть дорог устроена так: все города стоят на кольце; столица соединена отдельными ветками с каждым из городов, кроме соседей по кольцу. Правительство разбило сеть дорог на участки между соседними городами и постановило разделить эти участки между двумя компаниями так, чтобы можно было проехать между любыми двумя городами как по дорогам только первой компании, так и по дорогам только второй компании. Можно ли выполнить это постановление?
Задача 4.
В колоде часть карт лежит рубашкой вниз. Время от времени Петя вынимает из колоды пачку из одной или нескольких подряд идущих карт, в которой верхняя и нижняя карты лежат рубашкой вниз, переворачивает всю пачку как одно целое и вставляет в то же место колоды. Докажите, что в конце концов все карты лягут рубашкой вверх. (Примечание: если «пачка» состоит лишь из одной карты, то требуется только, чтобы она лежала рубашкой вниз.)
Задача 5.
В восьми корзинах лежали яблоки трех сортов: антоновка, джонатан и ранет, причем в каждой корзине – яблоки только одного сорта. В первой корзине лежало 20 яблок, во второй – 24, в третьей – 28, в четвертой – 32, в пятой – 36, в шестой – 40, в седьмой – 44, в восьмой – 48. После того как продали корзину ранета, яблок этого сорта осталось вдвое больше, чем антоновки, но вдвое меньше, чем джонатана. В каких корзинах лежала антоновка, а в каких ранет?
Задача 6.
В прямоугольнике 5 х 6 закрашено 19 клеток. Докажите, что в нем можно выбрать квадрат 2 х 2, в котором закрашено не менее трех клеток.
Задача 7.
На олимпиаду по математике съехалось n школьников. Оказалось, что среди любых пяти из них найдется по крайней мере один, знакомый со всеми остальными из этой пятерки. При каких n отсюда можно заключить, что на олимпиаде присутствует школьник, знакомый со всеми участниками олимпиады?

























