прямо пропорциональный
Смотреть что такое «прямо пропорциональный» в других словарях:
прямо пропорциональный — — Тематики электротехника, основные понятия EN directly proportional … Справочник технического переводчика
прямо пропорциональный — пр ямо пропорцион альный … Русский орфографический словарь
прямо пропорциональный — … Орфографический словарь русского языка
ПРОПОРЦИОНАЛЬНЫЙ — (лат. proportionalis от proportio отношение, сходство, пропорция). Соразмерный, правомерный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНЫЙ лат. propotiornalis, от proportio, пропорция.… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНЫЙ — ПРОПОРЦИОНАЛЬНЫЙ, пропорциональная, пропорциональное; пропорционален, пропорциональна, пропорционально (лат. proporcionalis соразмерный) (книжн.). 1. Обладающий соразмерностью частей. Пропорциональное телосложение. 2. Такой, который с увеличением … Толковый словарь Ушакова
пропорциональный детектор ионизирующего излучения — пропорциональный детектор Детектор ионизирующего излучения, у которого выходной сигнал прямо пропорционален некоторой физической величине, характеризующей излучение. Примечание Обычно такой физической величиной является энергия, потерянная… … Справочник технического переводчика
пропорциональный закон регулирования — пропорциональный закон управления П закон Линейный закон управления, отражающий прямо пропорциональную зависимость значения управляющего воздействия от значения воздействия отклонения. [Сборник рекомендуемых терминов. Выпуск 107. Теория… … Справочник технического переводчика
ПРОПОРЦИОНАЛЬНЫЙ ДОГОВОР (ДОГОВОР КВОТНОГО ПЕРЕСТРАХОВАНИЯ) — (proportional treaty, quota share reinsurance treaty) Соглашение по перестрахованию (reinsurance), в соответствии с которым риски распределяются прямо пропорционально выплаченным страховым взносам. Финансы. Толковый словарь. 2 е изд. М.: ИНФРА М … Финансовый словарь
пропорциональный закон управления — пропорциональный закон управления; п закон Линейный закон управления, отражающий прямо пропорциональную зависимость значения управляющего воздействия от значения воздействия отклонения … Политехнический терминологический толковый словарь
Как пишется “прямо пропорциональный” или “прямопропорциональный”?
Как писать правильно слово “прямо пропорциональный” или “прямопропорциональный”? Какое правило?
Пишется раздельно. Можно задать вопрос – какой? “Пропорциональный”. Как? “Прямо”. Это как “темно-красный”, только здесь через дефис. К тому же, есть слово “пропорциональный”, значит без части “прямо” это слово может существовать, т.е. пишется раздельно. Ну и можно посмотреть по наречию, “прямо пропорционально” тоже пишется раздельно, а значит и “прямо пропорциональный” будет тоже писаться раздельно.
Следует различать сложные прилагательные и сочетания слов, первое из которых является, как правило, наречием, а второе прилагательным. Часто первое слово-наречие, это такие слова, как “абсолютно”, “строго”, “сугубо”, “прямо” и др.
Сочетание “прямо пропорциональный” является именно таким случаем. Слово “прямо” – это наречие, отвечает на вопрос “как?”. А второе слово “пропорциональный” – это прилагательное, которое должно писаться с наречием раздельно.
Вывод – сочетание “прямо пропорционально” пишется раздельно.
Здесь правило довольно простое: “Мягкий знак “ь” после шипящих пишется только у существительных женского рода”. Сравни: “мышь”, “ложь”, “помощь” и др.
Слово “палач” – мужского рода, следовательно мягкий знак здесь не пишется.
Правильно: неприязненный.
Из словря: ПРИЯЗНЬ, Устар. Дружеское расположение к кому-л., симпатия. НЕПРИЯЗНЬ, Недружелюбное, недоброжелательное, враждебное чувство к кому-, чему-л.
Итак, когда-то существовало слово “приязнь”, которое теперь устарело, и от него с помощью приставки НЕ образовалось существительное “неприязнь”, которое не только не устарело, а даже весьма употребительно в современном языке.
Схема образования прилагательного “неприязненный” такова: приязнь – неприязнь – неприязненный, поэтому приставка НЕ может писаться только слитно, так как прилагательного “приязненный” не существует.
Правильно: антенка, антенщик, хотя антенна.
Обычно двойные согласные в производных словах сохраняются, но в виде исключения происходит усечение согласных перед суффиксом на согласную. Это делается, чтобы избежать стечения большого количества согласных.
В качестве другого примера можно привести производные слова от “кристалл”: кристаллический, кристаллик, но: кристальный, кристально.
Также в именах: Алла – Алка, Анна – Анка. Кирилл – Кирилка.
Существует правило – сложные местоимения, вторая часть которых является «либо», всегда пишутся через дефис.
Рассмотри слово «кого-либо». Это сложное местоимение, первая часть – «кого», вторая часть – «либо». По вышеуказанному правилу местоимение «кого-либо» должно всегда писаться через дефис.
Вывод – слово «кого-либо» пишется через дефис.
Пишется раздельно. Полдень – это существительное, а за – это предлог. Предлоги в отличии от приставок пишутся раздельно. Предлог – это служебная часть речи, которая выражает зависимость существительных, числительных и местоимений от других слов в словосочетаниях и предложениях.
Прямая пропорциональность
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
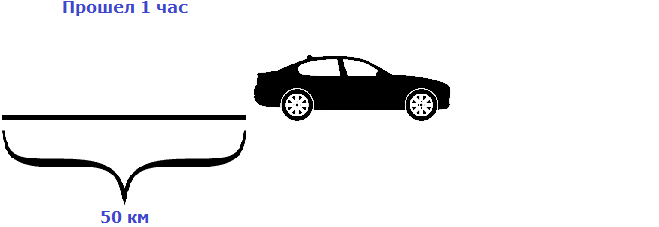
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
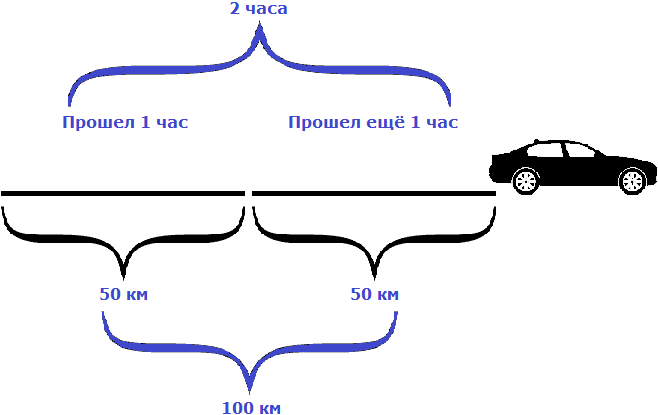
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Что такое прямая пропорциональность?
Прямая пропорциональность можно записать в виде уравнения: y = kx, где y и x — величины, k — постоянное значение, означающее отношение между y и x. Коэффициент пропорциональности k показывает, насколько y изменяется при изменении x на единицу.
Примеры прямой пропорциональности:
- Количество пройденных километров зависит от количества затраченного топлива. Чем больше топлива используется, тем больше километров пройдено.
- Время работы зависит от количества рабочей силы. Чем больше рабочих, тем больше времени потребуется для выполнения задачи.
- Стоимость товара зависит от количества единиц товара. Чем больше товаров покупается, тем выше стоимость покупки.
Прямая пропорциональность используется во многих областях, включая физику, экономику и инженерию. Эта концепция помогает анализировать и предсказывать взаимосвязи между величинами и решать различные задачи.
Морфологический разбор глагола
- начальная форма — инфинитив;
- постоянные морфологические признаки глагола:
-
- переходность:
-
- переходный (употребляется с существительными винительного падежа без предлога);
- непереходный (не употребляется с существительным в винительном падеже без предлога);
- возвратность:
-
- возвратные (есть -ся, -сь);
- невозвратные (нет -ся, -сь);
- вид:
-
- несовершенный (что делать?);
- совершенный (что сделать?);
- спряжение:
-
- I спряжение (дела-ешь, дела-ет, дела-ем, дела-ете, дела-ют/ут);
- II спряжение (сто-ишь, сто-ит, сто-им, сто-ите, сто-ят/ат);
- разноспрягаемые глаголы (хотеть, бежать);
- непостоянные морфологические признаки глагола:
-
- наклонение:
-
- изъявительное: что делал? что сделал? что делает? что сделает?;
- условное: что делал бы? что сделал бы?;
- повелительное: делай!;
- время (в изъявительном наклонении: прошедшее/настоящее/будущее);
- лицо (в настоящем/будущем времени, изъявительного и повелительного наклонения: 1 лицо: я/мы, 2 лицо: ты/вы, 3 лицо: он/они);
- род (в прошедшем времени, единственного числа, изъявительного и условного наклонения);
- число;
- синтаксическая роль в предложении. Инфинитив может быть любым членом предложения:
-
- сказуемым: Быть сегодня празднику;
- подлежащим :Учиться всегда пригодится;
- дополнением: Все гости просили ее станцевать;
- определением: У него возникло непреодолимое желание поесть;
- обстоятельством: Я вышел пройтись.
Выбор между «прямо пропорционально» и «прямопропорционально»
Правильное написание фразы «прямо пропорционально» вызывает неоднозначность и споры среди носителей русского языка. Некоторые предпочитают разделять слова и писать их отдельно, то есть «прямо» и «пропорционально». Другие же склонны писать слова слитно: «прямопропорционально».
Мнение о том, какой вариант правильный, поддерживается исходя из того, что есть логичным. Однако, стоит учесть, что традиционно слова «прямо» и «пропорционально» пишутся отдельно. В русском языке есть множество примеров, когда подобные конструкции пишутся раздельно. Например, «быстро управлять», «медленно плавать» и т.д. Таким образом, вариант с разделением слов является более соответствующим правилам русской орфографии.
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Вопрос-ответ:
Что такое прямая пропорциональность?
Прямая пропорциональность — это связь между двумя величинами, при которой их отношение остается постоянным. То есть, если одна величина увеличивается или уменьшается в некоторое количество раз, то и вторая величина также увеличивается или уменьшается в то же самое количество раз.
Какие примеры прямой пропорциональности можно привести?
Примеры прямой пропорциональности встречаются в различных ситуациях. Например, если время, затрачиваемое на проезд определенного расстояния, увеличивается в два раза, то и средняя скорость движения уменьшается в два раза. Также это может быть отношение между количеством работы и временем, затрачиваемым на ее выполнение, или между площадью прямоугольника и длиной его стороны.
Как можно определить прямую пропорциональность величин?
Для определения прямой пропорциональности величин необходимо проверить, остается ли их отношение постоянным при изменении одной из них. Если отношение остается неизменным, то можно говорить о прямой пропорциональности. Например, если при увеличении времени проезда расстояние увеличивается в том же отношении, то это будет прямая пропорциональность.
Как работает прямая пропорциональность в математике?
В математике прямая пропорциональность может быть выражена с помощью формулы y = kx, где y — зависимая величина, x — независимая величина, а k — постоянная пропорциональности. При увеличении значения x в k раз, значение y увеличивается в k раз. Это позволяет подобрать нужное значение k для соответствующих величин и решить задачу на прямую пропорциональность.
Как связано понятие прямой пропорциональности с решением задач?
Понимание прямой пропорциональности позволяет более легко решать задачи, связанные с изменением величин. Зная, что две величины связаны прямо пропорционально, можно использовать соответствующую формулу или методику для нахождения нужного значения. Это помогает более эффективно и точно решать задачи в различных областях, как математических, так и практических.
Что такое прямая пропорциональность?
Прямая пропорциональность — это математическое понятие, которое описывает зависимость двух величин, при которой они изменяются пропорционально друг другу. То есть, если одна величина увеличивается в некоторое количество раз, то и вторая величина также увеличивается в том же количество раз.
Какие примеры прямой пропорциональности можно привести?
Примеры прямой пропорциональности можно найти в различных областях. Например, если производитель выпускает в 2 раза больше продукции, то его прибыль также будет увеличиваться в 2 раза. Другой пример — расстояние, пройденное автомобилем и время поездки. Если автомобиль движется со скоростью 60 км/ч, то за 2 часа он пройдет 120 км.
Post Views: 14
Определение и различие
Слово пропорциональный означает, что две величины или два явления связаны друг с другом в определенной пропорции, то есть они изменяются вместе. В таком отношении они называются пропорциональными.
Слово прямопропорциональный имеет более узкое значение. Оно означает, что две величины или два явления движутся в одном направлении и изменяются в одной и той же пропорции. То есть, если одна величина увеличивается или уменьшается, то и другая величина меняется согласно этой пропорции.
Важно понимать, что прямопропорциональный – это один из видов пропорциональности. Он является частным случаем пропорциональности, где две величины движутся в одном направлении и изменяются одинаково
Понятие «прямо пропорциональный»
Выражение «прямо пропорциональный» относится к математическому понятию, которое описывает связь между двумя величинами. Если две величины прямопропорциональны, то они изменяются таким образом, что при увеличении одной величины, другая также увеличивается, и при уменьшении одной величины, другая также уменьшается.
Однако, следует обратить внимание на то, что в данном случае правильное написание заключается в том, чтобы использовать два слова, разделив их пробелом. Таким образом, корректное написание данного понятия будет следующим: «прямо пропорциональный»
Понятие «прямопропорциональный»
| Величина A | Величина B |
| 10 | 5 |
| 20 | 10 |
| 30 | 15 |
В таблице представлен пример прямопропорциональной зависимости между величинами A и B. Как видно, если A увеличивается вдвое, то B также увеличивается вдвое. Такая зависимость характеризует прямопропорциональность и может быть представлена графически прямой линией.
Как правильно оформлять орфограмму
Если «нечто» или «ничто» вы написали слитно, но надо подчеркнуть одной чертой сочетания букв «еч», «ич», выделить приставки не/ни и корень «что», а в скобках подписать: «нет предлога».
Если предлог есть, то «пробелы» перед ним и после него надо подчеркнуть одной чертой, а сам предлог – двумя. Этого будет достаточно.
Вслух можно проговорить следующее: «Отрицательное местоимение «ничто» пишется слитно, потому что не разделено предлогом».
Если вам надо объяснить, почему в приставке «е» или «и» то можно просто поставить ударение и выделить место орфограммы – приставку.
Если буква пропущена в частице, то выделять ее как приставку ни в коем случае не надо. Просто подчеркните букву одной чертой и надпишите ударение сверху.
Если у вас не получается объяснять орфограммы или вы не знаете, как это делать, прочитайте мою статью. И посмотрите вот это видео, оно тоже мое.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:

Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
План морфологического разбора существительного
Пример:
«Малыш пьет молоко.»
Малыш (отвечает на вопрос кто?) – имя существительное;
- начальная форма – малыш;
- постоянные морфологические признаки: одушевленное, нарицательное, конкретное, мужского рода, I -го склонения;
- непостоянные морфологические признаки: именительный падеж, единственное число;
- при синтаксическом разборе предложения выполняет роль подлежащего.
Морфологический разбор слова «молоко» (отвечает на вопрос кого? Что?).
- начальная форма – молоко;
- постоянная морфологическая характеристика слова: среднего рода, неодушевленное, вещественное, нарицательное, II -е склонение;
- изменяемые признаки морфологические: винительный падеж, единственное число;
- в предложении прямое дополнение.
Приводим ещё один образец, как сделать морфологический разбор существительного, на основе литературного источника:
«Две дамы подбежали к Лужину и помогли ему встать. Он ладонью стал сбивать пыль с пальто. (пример из: «Защита Лужина», Владимир Набоков).»
Дамы (кто?) — имя существительное;
- начальная форма — дама;
- постоянные морфологические признаки: нарицательное, одушевленное, конкретное, женского рода, I склонения;
- непостоянная морфологическая характеристика существительного: единственное число, родительный падеж;
- синтаксическая роль: часть подлежащего.
Лужину (кому?) — имя существительное;
- начальная форма — Лужин;
- верная морфологическая характеристика слова: имя собственное, одушевленное, конкретное, мужского рода, смешанного склонения;
- непостоянные морфологические признаки существительного: единственное число, дательного падежа;
- синтаксическая роль: дополнение.
Ладонью (чем?) — имя существительное;
- начальная форма — ладонь;
- постоянные морфологические признаки: женского рода, неодушевлённое, нарицательное, конкретное, I склонения;
- непостоянные морфо. признаки: единственного числа, творительного падежа;
- синтаксическая роль в контексте: дополнение.
Пыль (что?) — имя существительное;
- начальная форма — пыль;
- основные морфологические признаки: нарицательное, вещественное, женского рода, единственного числа, одушевленное не охарактеризовано, III склонения (существительное с нулевым окончанием);
- непостоянная морфологическая характеристика слова: винительный падеж;
- синтаксическая роль: дополнение.
(с) Пальто (С чего?) — существительное;
- начальная форма — пальто;
- постоянная правильная морфологическая характеристика слова: неодушевленное, нарицательное, конкретное, среднего рода, несклоняемое;
- морфологические признаки непостоянные: число по контексту невозможно определить, родительного падежа;
- синтаксическая роль как члена предложения: дополнение.
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Как пишется «прямо пропорциональный» или «прямопропорциональный»?
Как писать правильно слово «прямо пропорциональный» или «прямопропорциональный»? Какое правило?
Следует различать сложные прилагательные и сочетания слов, первое из которых является, как правило, наречием, а второе прилагательным. Часто первое слово-наречие, это такие слова, как «абсолютно», «строго», «сугубо», «прямо» и др.
Чтобы правильно написать заданное слово, стоит разобраться, как же образовалось оно.
Это слово собственно-русское.
И его образование является результатом сращения слова «пьрво», имевшего значение «сначала, прежде»,
и слова «зьданьныи» в значении «созданный», которое произведено от слова «зьдати» (строить, создавать). Родственными словами раньше были существительные «здание», «зодчий», но в современном языке русском слово первозданный, имеющее значение «созданного, существовавшего раньше всего остального», потеряло смысловую связь с указанными родственными словами, осталось только написание слова с той же согласной з во второй части.
Ну, а тому, кто не хочет обращаться к этимологии, нужно обратиться к словарю орфографическому и запомнить.
Туристы сбились с маршрута, но не пожалели об этом, потому что перед их взорами открылась первозданная красота удивительнейшего места, в которое, казалось, не ступала нога человека.






























